Mathematics 265 Introduction to Calculus I

Study Guide :: Appendix C

Correct Solutions: Learning from Mistakes

Unit 1

1. If $x$ is any number in the interval $[4,\infty)$, in which interval is $1 - \displaystyle{\frac{x}{2}}$?

   Mistake

   An inequality changes when it is multiplied (or divided) by a negative number.

   Solution

   If $x$ is in $[4,\infty)$, then $4 \le x$, and $-4 \ge -x$; thus $-2 \ge \displaystyle{\frac{-x}{2}}$. Therefore, $-1 \ge 1 - \displaystyle{\frac{x}{2}}$, and we conclude that $1 - \displaystyle{\frac{x}{2}}$ is in the interval $(-\infty,-1]$.

2. Simplify the following expressions.

   1. $(a + 3b)^2ab^{-1}$
   2. $(x^3y^{-3})^2$
   3. $(ab^2 - bc^3)abc$

   Mistake

   Improper use of the laws of exponents.

   It is not true that $(a + b)^n = a^n + b^n$, or that $(x^n)^r = x^{n + r}$.

   Solution

   1. $\begin{array}{rl}(a+3b{)}^{2}a{b}^{-<!--\; -\; -->1}& =(a^2+6ab+9b^2)a{b}^{-<!--\; -\; -->1}\\ & =a^3{b}^{-<!--\; -\; -->1}+6a^2+9ab\\ & ={\displaystyle {\displaystyle \frac{a^3}{b}}+6a^2+9ab\text{.}}\end{array}$
   2. $(x^3y^{-3})^2 = x^6y^{-6} = \displaystyle{\frac{x^6}{y^6}}$.
   3. $(ab^2 - bc^3)abc = a^2b^3c - ab^2c^4$.
3. Factor the following expressions.
   1. $2x^2 - 7x - 4$
   2. $3x^5 + 24x^2$
   3. $81x^4y - y^5$

   Mistake

   Improper use of the factorization rules.

   It is not true that $2x^2 - 7x - 4 = (x - 4)(x + \displaystyle{\frac{1}{2}})$, or that $(x^3 + 8) = (x + 2)(x^2 + 2x + 4)$. In part (c), the factorization of $\sqrt{y}$ is incorrect.

   Solution

   1. By the quadratic formula,

      $\displaystyle{x = \frac{7 \pm \sqrt{49 - 4(2)(-4)}}{4} = \frac{7 \pm 9}{4}} \textrm{;}$

      hence, the solutions are $ x = 4$ and $x = -\displaystyle{\frac{1}{2}}$, and the factors are

      $x^2 - \displaystyle{\frac{7}{2}}x - 2 = (x - 4)(x + \displaystyle{\frac{1}{2}})\textrm{.}$

      However, $2x^2 - 7x - 4 = (x - 4)(2x + 1)$.

   2. $3x^5 + 24x^2 = 3x^2(x^3 + 8) = 3x^2(x + 2)(x^2 - 2x + 4)$

   3. $\begin{array}{rl}81x^{4}y-<!--\; -\; -->y^5& =(9x^2\sqrt{y}-<!--\; -\; -->y^{5/2})(9x^2\sqrt{y}+y^{5/2})\\ & =\sqrt{y}(9x^2+y^2)\sqrt{y}(9x^2-<!--\; -\; -->y^2)\\ & =y(3x-<!--\; -\; -->y)(3x+y)(9x^2+y^2)\end{array}$

      Another way:

      \begin{align*} y(81x^4 - y^4) & = y(9x^2 - y^2)(9x^2 + y^2)\\ & = y(3x - y)(3x + y)(9x^2 + y^2)\textrm{.} \end{align*}

4. 1. Simplify the expression $\displaystyle{\frac{x^2 + 9x + 20}{x^2 + 5x}}\textrm{.}$
   2. Rationalize the expression $\displaystyle{\frac{\sqrt{4 + h}-2}{h}}\textrm{.}$

   Mistake

   Improper cancelation in rational expressions.

   It is not true that $\displaystyle{\frac{x^2 + 9x + 20}{x^2 + 5x} = \frac{9x + 20}{5x}}$, or that $\sqrt{4 + h} = 2 + \sqrt{h}$.

   Solution

   1. $\displaystyle{\frac{x^2 + 9x + 20}{x^2 + 5x} = \frac{(x + 5)(x + 4)}{x(x + 5)} = \frac{x + 4}{x}}$, for $x \neq 0$ and $x \neq -5$.
   2. $\begin{array}{rl}{\displaystyle \frac{\sqrt{4+h}-<!--\; -\; -->2}{h}}& ={\displaystyle \frac{(\sqrt{4+h}-<!--\; -\; -->2)(\sqrt{4+h}+2)}{h(\sqrt{4+h}+2)}}\\ & ={\displaystyle \frac{4+h-<!--\; -\; -->4}{h(\sqrt{4+h}+2)}}\\ & ={\displaystyle \frac{1}{\sqrt{4+h}+2}}\text{.}\end{array}$
5. Give the exact values of each of the following trigonometric functions.
   1. $\sec \left(\displaystyle{\frac{7\pi}{6}}\right)$
   2. $\sin \left(\displaystyle{\frac{7\pi}{12}}\right)$

   Mistake

   It is not true that $\displaystyle{\cos\left(\frac{7\pi}{6}\right) = \cos\left(\frac{\pi}{6}\right)}$, or that $\displaystyle{\sin\left(\frac{\pi}{3} + \frac{\pi}{4}\right) = \sin\left(\frac{\pi}{3}\right) + \sin\left(\frac{\pi}{4}\right)}$.

   Solution

   1. $\displaystyle{\sec \left(\displaystyle{\frac{7\pi}{6}}\right) = \frac{1}{\cos \left(\displaystyle{\frac{7\pi}{6}}\right)}= \frac{1}{-\cos \left(\displaystyle{\frac{\pi}{6}}\right)}}$

      $\hspace{4.6em}\displaystyle{= -\frac{1}{\sqrt{3}/2} = -\frac{2\sqrt{3}}{3}}$.

   2. $\displaystyle{\sin \left(\frac{7\pi}{12}\right) = \sin \left(\frac{\pi}{3} + \frac{\pi}{4}\right)}$

      $\hspace{4.6em}\displaystyle{= \sin \left(\frac{\pi}{3}\right)\cos\left(\frac{\pi}{4}\right) + \sin \left(\frac{\pi}{4}\right)\cos\left(\frac{\pi}{3}\right)}$

      $\hspace{4.6em}\displaystyle{= \frac{\sqrt{3}}{2}\frac{1}{\sqrt{2}} + \frac{\sqrt{2}}{2}\frac{1}{2} = \frac{\sqrt{3} + 1}{2\sqrt{2}}}$

Unit 2

1. Define each of the functions below as a set of pairs.
   1. The velocity $v$ depends on the time $t$.
   2. The bacteria population $B$ depends on the amount of oxygen $o$.

   Mistake

   The order of the variables is incorrect. In part (b) the variable $B$ depends on the variable $o$.

   Solution

   1. $\{ (t,v)|v\;{\text{is}}\;{\text{the}}\;{\text{velocity}}\;{\text{at}}\;{\text{time}}\;t\}$
   2. $\{(o,B)|B\;{\text{is}}\;{\text{the}}\;{\text{population}}\;{\text{for}}\;{\text{the}}\;{\text{amount}}\;{\text{of}}\;{\text{oxygen}}\;o\}$

2. Let $S(t) = 3.75t^2 + 500$ be a function, where $S$ is the salary for the number of units sold $t$. Find the value of $S$ at $t = 4 - \sqrt{14}$.

   Mistake

   It is not true that $(4 - \sqrt{14})^2 = 16 - 14$.

   Solution

   \begin{align*} S(4 - \sqrt{14}) & = 3.75(4 - \sqrt{14})^2 + 500\\ & = 3.75(16 - 8\sqrt{14} + 14) + 500 \\ & = 612.50 - 30\sqrt{14} \textrm{.} \end{align*}

3. Find the domain of each of the following functions.
   1. $g(t) = \displaystyle{\frac{4 - t}{6 - \sqrt{t^2 - 9}}}$
   2. $h(x) = \tan(2x)$

   Mistake

   In part (a) the denominator (i.e., that $6 - \sqrt{t^2 - 9}$) must be nonzero. In part (b) $\tan u$ is not defined for $u = \displaystyle{\frac{k\pi}{2}}$ for $k$ an odd integer.

   Solution

   1. We need $t^2 - 9 \ge 0$; hence, $t \ge 3$ and $t \le -3$. We also need $6 - \sqrt{t^2 -9} \neq 0$; so $t \neq \pm \sqrt{45}$. Therefore, the domain, in interval notation, is the union of the intervals, $(-\infty,-\sqrt{45})$, $(-\sqrt{45},-3]$, $[3,\sqrt{45})$ and $(\sqrt{45},\infty)$.
   2. Since $\tan(u)$ is undefined for $u = \displaystyle{\frac{k\pi}{2}}$, where $k$ is any odd integer, we need $2x \neq \displaystyle{\frac{k\pi}{2}}$, and $x \neq \displaystyle{\frac{k\pi}{4}}$. The domain is all numbers except $\displaystyle{\frac{k\pi}{4}}$ for any odd integer $k$.
4. Sketch the graph of a single function that satisfies all of the conditions listed below.
   1. The domain is $[3,12]$.
   2. The pairs $(4,5)$ and $(5,4)$ are in the function.
   3. The function is constant and equal to $1$ over the interval $(8,12]$.

   

   Figure 1. Erroneous solution to “Learning from Mistakes” Question 4.

   Mistake

   The graph does not show the points at the endpoints of the intervals.

   Solution

   The function must be defined for all numbers in the interval $[3,12]$; it is constant at $1$ on $(8,12]$.

   

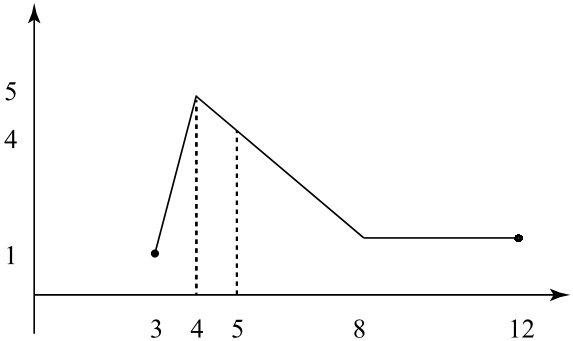
   Figure 2. Correct solution to “Learning from Mistakes” Question 4.

5. If the graph of the function $f$ is shown below, give a sketch of each of the following functions.
   1. $F(x) = 2f(x) - 1$
   2. $F(x) = f(x + 2) +3$.

   

   Figure 3. Graph for “Learning from Mistakes” Question 5.

   Mistake

   The transformations are incorrect.

   Solution

   1. The transformations are stretched by $2$ units first, and a shift down by $1$ unit second.

      

      Figure 4. Correct solution to “Learning from Mistakes” Question 5(a).

   2. The transformations are a shift by 2 units to the left first, and a shift up by $3$ units second.

      

      Figure 5. Correct solution to “Learning from Mistakes” Question 5(b).

      

Unit 3

1. Draw the graph of a single function $f$, such that
   1. $\displaystyle{\lim_{x \to 0}f(x) = 3}$
   2. $\displaystyle{\lim_{x \to -2}f(x) = \infty}$
   3. $\displaystyle{\lim_{x \to \infty}f(x) = -1.}$

   Mistake

   The graph given is not the graph of a function because it fails the vertical line test. A possible answer is given in the figure below.

   

   Figure 6. Correct solution to “Learning from Mistakes” Question 1.

   

   Figure 7. Graph for “Learning from Mistakes” Question 2.

2. Find the following limits for the function shown in Figure 7, above.
   1. $\displaystyle{\lim_{x \to -4^-}f(x)}$
   2. $\displaystyle{\lim_{x \to 2}f(x)}$
   3. $\displaystyle{\lim_{x \to \infty}f(x)}$
   4. $\displaystyle{\lim_{x \to -4^+} f(x)}$.

   Mistakes and Solutions

   1. The limit is from the left at $-4$; hence, it is $\infty$.
   2. Around $2$, the function increases (on the left of $2$) and decreases (on the right of $2$); hence, the limit does not exist.
   3. The limit at infinity is a horizontal asymptote, hence the limit is $1$.
   4. On the right of $4$, the function decreases without bounds, hence the limit is negative infinity.
3. Evaluate each of the following limits. If a limit does not exist, explain why.
   1. $\displaystyle{\lim_{x \to 0^+} x \sin x + \frac{1}{x}}$
   2. $\displaystyle{\lim_{x \to 1} \frac{x^2 + 2x - 15}{x^2 + x -12}}$
   3. $\displaystyle{\lim_{x \to 0} \frac{x^2 -1}{x^2 + x^4}}$
   4. $\displaystyle{\lim_{x \to \pi/2^-} \tan x + \sec x}$
   5. $\displaystyle{\lim_{x \to 0^+} \frac{\tan(3x)}{\sin(4x)}}$
   6. $\displaystyle{\lim_{x \to 3}\frac{\sin(x - 3)}{x^2 + x -12}}$
   7. $\displaystyle{\lim_{x \to \infty} x\cos\left(\frac{1}{x}\right)}$
   8. $\displaystyle{\lim_{x \to \infty} \frac{\cos x }{x}}$
   9. $\displaystyle{\lim_{x \to \infty} \frac{x^2 + 3}{\sqrt{x^2 + x - 1}}}$
   10. $\displaystyle{\lim_{x \to -\infty} \frac{\sqrt{(3x + 2)(x + 1)}}{3 - x}}$

   Mistakes and Solutions

   1. $\displaystyle{\lim_{x \to 0^+} x \sin x + \frac{1}{x}}$

      Mistake

      Incorrect use of the laws of limits (Theorem 3.23), because

      $\displaystyle{\lim_{x \to 0^+}\frac{1}{x} = \infty}.$

      Solution

      1. Identifying the definitions and results of this unit:

         $\displaystyle{\lim_{x \to 0^+} x \sin x = 0}$		by Theorem 3.14
         $\displaystyle{\lim_{x \to 0^+}\frac{1}{x} = \infty}$		by part (a) of Theorem 3.17
         $\displaystyle{\lim_{x \to 0^+} x \sin x + \frac{1}{x} = \infty}$		by Theorem 3.21.

      2. Without identifying the definitions and results of this unit:

         $\displaystyle{\lim_{x \to 0^+} x \sin x = 0\sin(0) = 0}$		since $x \sin x$ is an everywhere continuous function
         $\displaystyle{\lim_{x \to 0^+}\frac{1}{x} = \infty}$		since $\displaystyle{\lim_{x \to 0^+}x = 0}$ is an everywhere continuous function, and $x \gt 0$ for $x \to 0^+$

      Hence, $\displaystyle{\lim_{x \to 0^+} x \sin x + \frac{1}{x} = \infty}$.

   2. $\displaystyle{\lim_{x \to 1} \frac{x^2 + 2x - 15}{x^2 + x -12}}$

      Mistake

      $\displaystyle{\lim_{x \to 1} \frac{x^2 + 2x - 15}{x^2 + x -12} = \frac{(x -3)(x + 5)}{(x - 3)(x + 4)}}$ is an incorrect statement.

      Solution

      1. Identifying the definitions and results of this unit:

         $\displaystyle{\lim_{x \to 1} \frac{x^2 + 2x - 15}{x^2 + x -12}}$
         $\displaystyle{= \lim_{x \to 1}\frac{(x -3)(x + 5)}{(x - 3)(x + 4)} = \lim_{x \to 1} \frac{x + 5}{x + 4}}$		by Proposition 3.16
         $\displaystyle{=\frac{6}{5}}$		by Theorem 3.14.

      2. Without identifying the definitions and results of this unit:

         $\displaystyle{\lim_{x \to 1} \frac{x^2 + 2x - 15}{x^2 + x -12}}$
         $\displaystyle{= \lim_{x \to 1}\frac{(x -3)(x + 5)}{(x - 3)(x + 4)} = \lim_{x \to 1} \frac{x + 5}{x + 4}}$
         $\displaystyle{=\frac{6}{5}}$		Since $\displaystyle{\frac{x + 5}{x + 4}}$ is continuous at $1$

   3. $\displaystyle{\lim_{x \to 0} \frac{x^2 -1}{x^2 + x^4}}$

      Mistake

      It is incorrect to divide by zero, and the expression $\displaystyle{\frac{-1}{0} = \infty}$ is nonsense.

      Solution

      1. Identifying the definitions and results of this unit:

         $\displaystyle{\lim_{x \to 0} x^2 -1 = -1}$ and $\displaystyle{\lim_{x \to 0} x^2 + x^4 = 0}$		by Theorem 3.14.
         $\displaystyle{\lim_{x \to 0} \frac{1}{x^2 + x^4} = \infty}$		by Theorem 3.21, since $x^2 + x^4 \gt 0$ for $x \to 0$.
         $\displaystyle{\lim_{x \to 0} \frac{x^2 -1}{x^2 + x^4} = -\infty}$		by part (b) of Theorem 3.18.

      2. Without identifying the definitions and results of this unit.

         $\displaystyle{\lim_{x \to 0} \frac{x^2 -1}{x^2 + x^4}}$		because
         $\displaystyle{= \lim_{x \to 0} (x^2 -1)\frac{1}{x^2 + x^4} = \infty}$		1.  $\displaystyle{\lim_{x \to 0} x^2 -1 = -1 \lt 0}$, since $x^2 - 1$ is everywhere continuous.
         		2.  $\displaystyle{\lim_{x \to 0} \frac{1}{x^2 + x^4} = \infty}$, since $\displaystyle{\lim_{x \to 0} x^2 + x^4 = 0}$ and $x^2 + x^4 \gt 0$ for $x \to 0$.

   4. $\displaystyle{\lim_{x \to \pi/2^-} \tan x + \sec x}$

      Mistake

      It is incorrect to state that $\infty + \infty = \infty$, even when both limits are infinite.

      Solution

      1. Identifying the definitions and results of this unit:

         $\displaystyle{\lim_{x \to \pi/2^-} \tan x = \lim_{x \to \pi/2^-} (\sin x)\frac{1}{\cos x} = \lim_{x \to \pi/2^-} \sin x\,\sec x}$

         $\displaystyle{\lim_{x \to \pi/2^-} \sin x = \sin\left(\frac{\pi}{2}\right) = 1}$ and
         $\displaystyle{\lim_{x \to \pi/2^-} \cos x = \cos\left(\frac{\pi}{2}\right) = 0}$		by Theorem 3.14.
         $\displaystyle{\lim_{x \to \pi/2^-} \frac{1}{\cos x} = \infty}$		by part (a) of Theorem 3.17, since $\cos x \gt 0$ for $\displaystyle{x \to \frac{\pi}{2^-}}$
         Hence,
         $\displaystyle{\lim_{x \to \pi/2^-} \tan x = \infty = \lim_{x \to \pi/2^-} \sec x}$		by Theorem 3.18.
         Therefore,
         $\displaystyle{\lim_{x \to \pi/2^-} \tan x + \sec x = \infty}$		by part (a) of Theorem 3.21.

      2. Without identifying the definitions and results of this unit.

         $\displaystyle{\lim_{x \to \pi/2^-} \tan x = \lim_{x \to \pi/2^-} (\sin x)\frac{1}{\cos x} = \lim_{x \to \pi/2^-} \sin x\,\sec x}$

         $\displaystyle{\lim_{x \to \pi/2^-} \sin x = \sin\left(\frac{\pi}{2}\right) = 1 \gt 0}$		since $\sin x$ is continuous everywhere.
         $\displaystyle{\lim_{x \to \pi/2^-} \frac{1}{\cos x} = \lim_{x \to \pi/2^-} \sec x = \infty}$		since $\displaystyle{\lim_{x \to \pi/2^-} \cos x = \cos\left(\frac{\pi}{2}\right) = 0}$ and $\cos x \gt 0$ for $\displaystyle{x \to \frac{\pi}{2^-}}$.
         xx		xx

         Hence,

         $\displaystyle{\lim_{x \to \pi/2^-} \tan x = \infty = \lim_{x \to \pi/2^-} \sec x}$,

         Therefore,

         $\displaystyle{\lim_{x \to \pi/2^-} \tan x + \sec x = \infty}$

   5. $\displaystyle{\lim_{x \to 0^+} \frac{\tan(3x)}{\sin(4x)}}$

      Mistake

      A side limit always exists so the answer is incorrect. It is also incorrect to write $\displaystyle{\frac{0}{0}}$; this expression is nonsense.

      Solution

      1. Identifying the definitions and results of this unit:

         $\displaystyle{\lim_{x \to 0^+} \frac{\tan(3x)}{\sin(4x)} = \lim_{x \to 0^+} \frac{\sin(3x)}{\sin(4x)}\frac{1}{\cos(3x)}}$

         $\displaystyle{\lim_{x \to 0^+} \frac{\sin(3x)}{\sin(4x)} = \frac{3}{4}}$		by Example 3.60
         $\displaystyle{\lim_{x \to 0^+} \frac{1}{\cos(3x)} = \frac{1}{\cos (0)} = 1}$		by Theorem 3.14
         $\displaystyle{\lim_{x \to 0^+} \frac{\tan(3x)}{\sin(4x)}}$
         $\displaystyle{ = \lim_{x \to 0^+} \frac{\sin(3x)}{\sin(4x)}\lim_{x \to 0^+}\frac{1}{\cos(3x)} = \frac{3}{4}}$		by part (c) of Theorem 3.23

      2. Without identifying the definitions and results of this unit.

         \begin{align*} \lim_{x \to 0^+} \frac{\tan(3x)}{\sin(4x)} & = \lim_{x \to 0^+} \frac{\sin(3x)}{\sin(4x)}\frac{1}{\cos(3x)} \\ & = \lim_{x \to 0^+} \frac{\sin(3x)}{\sin(4x)}\lim_{x \to 0^+}\frac{1}{\cos(3x)} \\ & = \frac{3}{4}(1) \\ & = \frac{3}{4} \end{align*}

         We know that

         $\displaystyle{\lim_{x \to 0^+} \frac{\sin(3x)}{\sin(4x)} = \frac{3}{4}}$   and   $\displaystyle{\lim_{x \to 0^+} \frac{1}{\cos(3x)} = \frac{1}{\cos (0)} = 1}$,

         because cosine is continuous everywhere.

   6. $\displaystyle{\lim_{x \to 3}\frac{\sin(x - 3)}{x^2 + x -12}}$

      Mistake

      This type of “guessing” argument is deceiving, as you can see in this “solution” (see also Examples 4 and 5 on page 74 of the textbook). The only sure way to evaluate limits is by applying definitions and proven results.

      Solution

      1. Identifying the definitions and results of this unit:

         $\displaystyle{\lim_{x \to 3}\frac{\sin(x - 3)}{x^2 + x -12} = \lim_{x \to 3}\frac{\sin(x - 3)}{(x - 3)(x + 4)} = \lim_{x \to 3}\left(\frac{\sin(x - 3)}{x - 3}\right) \left(\frac{1}{x + 4}\right)}$

         If $u = x - 3$, then $u \to 0$ as $x \to 3$ and
         $\displaystyle{\lim_{x \to 3}\frac{\sin(x - 3)}{x - 3} = \lim_{x \to 3}\frac{\sin u}{u} = 1}$		by Theorem 3.24 and Example 3.56
         $\displaystyle{\lim_{x \to 3}\frac{1}{x + 4} = \frac{1}{7}}$		by Theorem 3.14
         Hence,
         $\displaystyle{\lim_{x \to 3}\frac{\sin(x - 3)}{x^2 + x -12}}$
         $\displaystyle{= \lim_{x \to 3}\frac{\sin(x - 3)}{x - 3} \lim_{x \to 3}\frac{1}{x + 4} = \frac{1}{7}}$		by part (c) of Theorem 3.23

      2. Without identifying the definitions and results of this unit:

         $\displaystyle{\lim_{x \to 3}\frac{\sin(x - 3)}{x^2 + x -12} = \lim_{x \to 3}\frac{\sin(x - 3)}{(x - 3)(x + 4)} = \lim_{x \to 3}\left(\frac{\sin(x - 3)}{x - 3}\right)\left(\frac{1}{x + 4}\right)}$

         If $u = x - 3$, then $u \to 0$ as $x \to 3$ and

         $\displaystyle{\lim_{x \to 3}\frac{\sin(x - 3)}{x - 3} = \lim_{x \to 3}\frac{\sin u}{u} = 1}$
         $\displaystyle{\lim_{x \to 3}\frac{1}{x + 4} = \frac{1}{3 + 4} = \frac{1}{7}}$		since $\displaystyle{\frac{1}{x + 4}}$ is continuous at $3$

         Hence, by part (c) of Theorem 3.23,

         $\displaystyle{\lim_{x \to 3}\frac{\sin(x - 3)}{x^2 + x -12} = \lim_{x \to 3}\frac{\sin(x - 3)}{x - 3} \lim_{x \to 3} \frac{1}{x + 4 } = (1)\frac{1}{7} = \frac{1}{7}}.$

   7. $\displaystyle{\lim_{x \to \infty} x\cos\left(\frac{1}{x}\right)}$

      Mistake

      The inequality $\displaystyle{ -1 \le \cos\left(\frac{1}{x}\right) \le 1}$ is correct for $x \to \infty$, and the limit $\displaystyle{\lim_{x \to \infty} x = \infty}$ is also correct, but $\displaystyle{\lim_{x \to \infty} -x = -\infty}$ by Theorem 3.21. Hence, the Squeeze Theorem does not apply.

      Solution

      1. Identifying the definitions and results of this unit:

         If $\displaystyle{u = \frac{1}{x}}$, then $u \to 0$ as $x \to \infty$		by Example 3.65.
         $\displaystyle{\lim_{x \to \infty} \cos\left(\frac{1}{x}\right) = \lim_{x \to 0} \cos u = \cos 0 = 1}$ and
         $\displaystyle{\lim_{x \to \infty} x = \infty}$		by Corollary 3.25
         Hence,
         $\displaystyle{\lim_{x \to \infty} x\cos\left(\frac{1}{x}\right) = \infty}$		by part (a) of Theorem 3.18.

      2. Without identifying the definitions and results of this unit:

         If $\displaystyle{u = \frac{1}{x}}$, then $u \to 0$ as $x \to \infty$; hence,

         $\displaystyle{\lim_{x \to \infty} \cos\left(\frac{1}{x}\right) = \lim_{x \to 0} \cos u = \cos 0 = 1 \gt 0}.$

         Since $\displaystyle{\lim_{x \to \infty} x = \infty}$, we conclude that

         $\displaystyle{\lim_{x \to \infty} x\cos\left(\frac{1}{x}\right) = \infty}.$

   8. $\displaystyle{\lim_{x \to \infty} \frac{\cos x }{x}}$

      Mistake

      It is true that $\displaystyle{\lim_{x \to \infty} \cos x}$ does not exists, but this not make the given limit also nonexistent.

      Solution

      1. Identifying the definitions and results of this unit:

         For $x \to \infty$, $x$ is positive, and since
         $-1 \le \cos x \le 1$,
         $\displaystyle{-\frac{1}{x} \le \frac{\cos x}{x} \le \frac{1}{x}}$, and

         $\displaystyle{\lim_{x \to \infty} \frac{1}{x} = 0 = \lim_{x \to \infty} -\frac{1}{x}}$		by Example 3.65
         Hence,
         $\displaystyle{\lim_{x \to \infty} \frac{\cos x }{x} = 0}$		by the Squeeze Theorem.

      2. Without identifying the definitions and results of this unit:

         For $x \to \infty$, $x$ is positive, and since $ -1 \le \cos x \le 1$, we know that

         $\displaystyle{-\frac{1}{x} \le \frac{\cos x}{x} \le \frac{1}{x}}.$

         Since

         $\displaystyle{\lim_{x \to \infty} \frac{1}{x} = 0 = \lim_{x \to \infty} -\frac{1}{x}},$

         we conclude that

         $\displaystyle{\lim_{x \to \infty} \frac{\cos x }{x} = 0}$

         by the Squeeze Theorem.

   9. $\displaystyle{\lim_{x \to \infty} \frac{x^2 + 3}{\sqrt{x^2 + xv - 1}}}$

      Mistake

      The answer is an attempt to use Theorem 3.29, but the function is not rational so the theorem does not apply.

      Solution

      1. Identifying the definitions and results of this unit:

         We know that $\sqrt{x^2} = x$ for $x \to \infty$, and

         \begin{align*} \frac{x^2 + 3}{\sqrt{x^2 + x - 1}} & = \frac{x^2(1 + 3/x^2)}{\sqrt{x^2(1 + 1/x - 1/x^2)}}\\ & = \frac{x^2(1 + 3/x^2)}{x\sqrt{(1 + 1/x - 1/x^2)}} \\ & = x\,\frac{(1 + 3/x^2)}{\sqrt{1 + 1/x - 1/x^2}} \end{align*}

         $\displaystyle{\lim_{x \to \infty}\frac{(1 + 3/x^2)}{\sqrt{1 + 1/x - 1/x^2}} = 1}$		by Example 65 and part (d) of Theorem 3.23
         Since $\displaystyle{\lim_{x \to \infty} x = \infty}$, we know that $\displaystyle{\lim_{x \to \infty} \frac{x^2 + 3}{\sqrt{x^2 + x - 1}} = \infty}$		by part (a) of Theorem 3.18.

      2. Without identifying the definitions and results of this unit:

         We know that $\sqrt{x^2} = x$ for $x \to \infty$, and

         \begin{align*} \frac{x^2 + 3}{\sqrt{x^2 + x - 1}} & = \frac{x^2(1 + 3/x^2)}{\sqrt{x^2(1 + 1/x - 1/x^2)}}\\ & = \frac{x^2(1 + 3/x^2)}{x\sqrt{(1 + 1/x - 1/x^2)}} \\ & = x\,\frac{(1 + 3/x^2)}{\sqrt{1 + 1/x - 1/x^2}} \end{align*}

         $\displaystyle{\lim_{x \to \infty}\frac{(1 + 3/x^2)}{\sqrt{1 + 1/x - 1/x^2}} = \frac{1 + 0}{\sqrt{1 + 0 - 0}} = 1}$

         and

         $\displaystyle{\lim_{x \to \infty} x = \infty}.$

         Hence,

         $\displaystyle{\lim_{x \to \infty} \frac{x^2 + 3}{\sqrt{x^2 + x - 1}} = \infty}.$

   10. $\displaystyle{\lim_{x \to -\infty} \frac{\sqrt{(3x + 2)(x + 1)}}{3 - x}}$

       Mistake

       The mistake is not taking into account that for $x \to -\infty$, $\sqrt{x^2} = -x$.

       Solution

       1. Identifying the definitions and results of this unit:

          \begin{align*} \frac{\sqrt{(3x + 2)(x + 1)}}{3 - x} & = \frac{\sqrt{3x^2 + 5x + 2}}{3 - x}\\ & = \frac{\sqrt{x^2\left(3 + \displaystyle{\frac{5}{x}} + \frac{2}{x^2}\right)}}{x\left(\displaystyle{\frac{3}{x}} - 1\right)}\\ & = \frac{-x\sqrt{3 + \displaystyle{\frac{5}{x} + \frac{2}{x^2}}}}{x\left(\displaystyle\frac{3}{x} - 1\right)}\\& = -\frac{\sqrt{3 + \displaystyle{\frac{5}{x}} + \frac{2}{x^2}}}{\displaystyle\frac{3}{x} - 1} \end{align*}

          $\displaystyle{\lim_{x \to -\infty} \frac{\sqrt{(3x + 2)(x + 1)}}{3 - x}}$
          $\displaystyle{ = \lim_{x \to -\infty}} -\frac{\sqrt{3 + \displaystyle{\frac{5}{x}} + \frac{2}{x^2}}}{\displaystyle{\frac{3}{x}} -1}$
          $\displaystyle{ = -\frac{\sqrt{3}}{-1} = \sqrt{3}}$		by Proposition 3.16, Example 3.65, Corollary 3.26 and part (d) of Theorem 3.23

       2. Without identifying the definitions and results of this unit:

          \begin{align*} \frac{\sqrt{(3x + 2)(x + 1)}}{3 - x} & = \frac{\sqrt{3x^2 + 5x + 2}}{3 - x}\\ & = \frac{\sqrt{x^2\left(3 + \displaystyle{\frac{5}{x}} + \frac{2}{x^2}\right)}}{x\left(\displaystyle{\frac{3}{x}} - 1\right)}\\ & = \frac{-x\sqrt{3 + \displaystyle{\frac{5}{x} + \frac{2}{x^2}}}}{x\left(\displaystyle\frac{3}{x} - 1\right)}\\ & = -\frac{\sqrt{3 + \displaystyle{\frac{5}{x}} + \frac{2}{x^2}}}{\displaystyle\frac{3}{x} - 1} \end{align*}

          \begin{align*} \lim_{x \to -\infty} \frac{\sqrt{(3x + 2)(x + 1)}}{3 - x} & = \lim_{x \to -\infty} -\frac{\sqrt{3 + \displaystyle{\frac{5}{x}} + \frac{2}{x^2}}}{\displaystyle{\frac{3}{x}} - 1} \\ & = -\frac{\sqrt{3 + 0 + 0}}{0 - 1} = \sqrt{3} \end{align*}

4. Find the vertical and horizontal asymptotes of the function

   $g(x) = \displaystyle{\frac{\sqrt{x^4 + 4x^3 + 4x^2}}{3x^2 +5x - 2}}.$

   Mistake and Solution

   It is true that the function is not defined at $\displaystyle{\frac{1}{3}}$ and $-2$; however, by Definition 3.19, for the function to have vertical asymptotes, the limit at these numbers must be infinite.

   \begin{align*} \frac{\sqrt{x^4 + 4x^3 + 4x^2}}{3x^2 +5x - 2} & = \frac{\sqrt{x^4 + 4x^3 + 4x^2}}{(3x - 1)(x + 2)}\\ & = \left(\frac{\sqrt{x^4 + 4x^3 + 4x^2}}{x + 2}\right)\left(\frac{1}{3x - 1}\right) \end{align*}

   $\displaystyle{\lim_{x \to 1/3}\frac{\sqrt{x^4 + 4x^3 + 4x^2}}{x + 2} = \frac{\sqrt{\displaystyle{\frac{1}{81}} + \frac{4}{27} + \frac{4}{9}}}{\displaystyle{\frac{1}{3} + 2}} \gt 0}$

   $\displaystyle{\lim_{x \to 1/3^+} \frac{1}{3x - 1} = \infty}$		since $3x - 1 \gt 0$ for $x \to 1/3^+$ and $\displaystyle{\lim_{x \to 1/3^+} 3x - 1 = 0}.$
   Hence,
   $\displaystyle{\lim_{x \to 1/3^+} \frac{\sqrt{x^4 + 4x^3 + 4x^2}}{3x^2 +5x - 2} = \infty}$		by Theorem 3.18
   and $\displaystyle{x = \frac{1}{3}}$ is a vertical asymptote.

   For

   \begin{align*} \frac{\sqrt{x^4 + 4x^3 + 4x^2}}{3x^2 +5x - 2} & = \left(\frac{\sqrt{x^2(x^2 + 4x + 4)}}{3x - 1}\right)\left(\frac{1}{x + 2}\right)\\ & = \left(\frac{\sqrt{x^2}\sqrt{(x + 2)^2}}{3x - 1}\right)\left(\frac{1}{x + 2}\right) \end{align*}

   we have two cases to consider.

   Case 1

   For $x \to -2^+$, we know that $x \lt 0$ and $x + 2 \gt 0$; hence,

   $\sqrt{x^2} = -x \ \mbox{ and } \ \sqrt{(x + 2)^2} = x + 2.$

   Therefore,

   \begin{align*} \frac{\sqrt{x^4 + 4x^3 + 4x^2}}{3x^2 +5x - 2} & = \left(\frac{-x(x + 2)}{3x - 1}\right)\left(\frac{1}{x + 2}\right)\\ & = -\frac{x}{3x - 1} \ \mbox{ for } x \neq -2 \end{align*}

   $\displaystyle{\lim_{x \to -2^+} \frac{\sqrt{x^4 + 4x^3 + 4x^2}}{3x^2 +5x - 2} = \lim_{x \to -2^+} -\frac{x}{3x - 1} = -\frac{2}{7}}$

   by Proposition 3.16 and Theorem 3.14.

   Case 2

   For $x \to -2^-$, we know that $x \lt 0$ and $x + 2 \lt 0$; hence,

   $\displaystyle{\frac{\sqrt{x^4 + 4x^3 + 4x^2}}{3x^2 +5x - 2} = \left(\frac{x(x + 2)}{3x - 1}\right)\left(\frac{1}{x + 2}\right) = \frac{x}{3x - 1}} \ \mbox{(Why?)}.$

   Therefore,

   $\displaystyle{\lim_{x \to -2^-} \frac{\sqrt{x^4 + 4x^3 + 4x^2}}{3x^2 +5x - 2} = \lim_{x \to -2^-} \frac{x}{3x - 1} = \frac{2}{7}}$

   by Proposition 3.16 and Theorem 3.14. The line $x = -2$ is not a vertical asymptote.

   For horizontal asymptotes we have

   \begin{align*} \frac{\sqrt{x^4 + 4x^3 + 4x^2}}{3x^2 +5x - 2} & = \frac{\sqrt{x^4(1 + \displaystyle{\frac{4}{x}} + \frac{4}{x^2})}}{x^2(3 + \displaystyle{\frac{5}{x}} - \frac{2}{x^2})}\\ & = \frac{x^2\sqrt{1 + \displaystyle{\frac{4}{x}} + \frac{4}{x^2}}}{x^2(3 + \displaystyle{\frac{5}{x}} - \frac{2}{x^2})} \\ & = \frac{\sqrt{1 + \displaystyle{\frac{4}{x}} + \frac{4}{x^2}}}{3 + \displaystyle{\frac{5}{x}} - \frac{2}{x^2}} \end{align*}

   $\displaystyle{\lim_{x \to \infty}\frac{\sqrt{x^4 + 4x^3 + 4x^2}}{3x^2 +5x - 2} = \lim_{x \to \infty} \frac{\sqrt{1 + \displaystyle{\frac{4}{x}} + \frac{4}{x^2}}}{3 + \displaystyle{\frac{5}{x}} - \frac{2}{x^2}} = \frac{1}{3}}$

   by Example 3.65, Corollary 3.26 and part (d) of Theorem 3.23.

   Hence $y = \displaystyle{\frac{1}{3}}$ is a horizontal asymptote.

   Observe that the limit for $x \to -\infty$ is also $\displaystyle{\frac{1}{3}}$.

Unit 4

1. The displacement (in km) of a moving car is given by $s(t) = 3t^3 + 4t -2$, where $t$ is measured in hours.
   1. Give the average velocity in the time period $[1,5]$.
   2. Give the two different interpretations of value found in part (a), above.
   3. Give the average velocity in the time period $[1,1 + h]$ for $h \gt 0$.

   Mistakes

   Parts a) and (c)—incorrect order of the quotient. Part (b)—it is not the velocity that is increasing or decreasing, it is the distance. The slope of the secant line is incorrect.

   Solutions

   1. $\displaystyle{\frac{s(1)-s(5)}{1-5} = \frac{(3 + 4 -2)- 3(125)- 4(5)+2}{1-5} = 97}$.

      The average velocity is $97$ km/h.

   2. The average velocity from $1$ to $5$ hours is $97$ km/h. On average, the distance is increasing at a rate of $97$ km/h. The slope of the secant line through $(1,5)$ and $(5,393)$ is $97$.
   3. $\displaystyle{\frac{s(1 + h) - s(1)}{h} = \frac{3(1+h)^3 +4(1+h) -2-5}{h}= 13 + 9h + 3h^2}$.
2. Use Definition $4.5$ of the Study Guide to find $\displaystyle{\frac{d}{dx} \frac{3}{x}}$.

   Mistake

   Errors in the algebraic manipulations and the missing term $\displaystyle{\lim_{h \to 0}}$.

   Solution

   $\displaystyle{\lim_{h \to 0} \frac{3(x + h)^{-1} -3(x^{-1})}{h} = \lim_{h \to 0} \frac{3x - 3(x + h)}{x(x + h)h} = \lim_{h \to 0}\frac{-3}{x(x + h)} = -\frac{3}{x^2}}$.

3. Consider the piecewise function

   \begin{equation*} f(x) = \left\{ \begin{array}{ll} |x| & \mbox{for $x \leq 4$}\\ (x - 6)^2 & \mbox{for $x \gt 4$} \end{array} \right. \end{equation*}

   1. Sketch the graph of the function $f$.
   2. Sketch the graph of the derivative function $f'$.

   Mistake

   There is no mistake in part (a). In part (b), the derivative function for $x \gt 4$ is incorrect. For $4 \lt x \lt 6$ the derivative is negative, and for $x \gt 6$ the derivative is positive.

   Solution

   

   Figure 8. Correct solution to “Learning from Mistakes” Question 3(a).

   

   Figure 9. Correct solution to “Learning from Mistakes” Question 3(b).

4. Find the derivatives indicated below.

   1. $\displaystyle{f(x) = \frac{3x^2 + 6x - 3}{x -4x^3}}$,   find $f'(x)$.
   2. $\displaystyle{\frac{d}{dx}\; \sqrt{x^3\sin x}}$.
   3. $\displaystyle{\frac{d}{dx}\; \sec{\sqrt{x + 1}}}$.
   4. $\displaystyle{\frac{d^2}{dx^2}\; \tan(3x)}$.

   Mistakes and Solutions

   1. Mistake

      The numerator of the quotient is in the wrong order.

      Solution

      $f'(x) = \displaystyle{\frac{(6x + 6)(x -4x^3)-(3x^2 + 6x - 3)(1 -12x^2)}{(x-4x^3)^2}}.$

   2. Mistake

      The derivative of $x^3\sin x$ is incorrect.

      Solution

      $\displaystyle{\frac{d}{dx}\; \sqrt{x^3\sin x} = \frac{3x^2\sin x +x^3\cos x}{2\sqrt{x^3\sin x}}}.$

   3. Mistake

      The chain rule is not applied properly.

      Solution

      $\displaystyle{\frac{d}{dx}\; \sec{\sqrt{x + 1}} = \sec \sqrt{x + 1} \tan \sqrt{x + 1} \left(\frac{1}{2\sqrt{x + 1}}\right)}.$

   4. Mistake

      The chain rule is not applied properly.

      Solution

      $\displaystyle{\frac{d}{dx}}\; \tan(3x) = 3\sec^2(3x)$ and $\displaystyle{\frac{d}{dx}}\; 3\sec^2(3x) = 18\sec^2(3x)\tan(3x).$

5. A particle is moving along the curve $y = \sqrt{x}$. As the particle passes through the point $(4,2)$, its $x$-coordinate increases at a rate of $3$ cm/s. How fast is the distance from the particle to the origin changing at this instant?

   Mistake

   Here $x$ is changing with respect to time, so the implicit differentiation is incorrect.

   Solution

   We know that $\displaystyle{\frac{dx}{dt} = 3}$, and we want to know $\displaystyle{\frac{dD}{dt}}$ when $x = 4$, where $D$ is the distance from the origin to the point $(x,y)$ on the curve.

   Hence, $D = \sqrt{x^2 + y^2}$. Differentiating yields

   $\displaystyle{\frac{dD}{dt} = \frac{2x\displaystyle{\frac{dx}{dt}} + 2y\frac{dy}{dt}}{2\sqrt{x^2 + y^2}}}.$

   For $x = 4$ and $\displaystyle{\frac{dx}{dt}} = 3$, we have $y' = \displaystyle{{x'} \over {2\sqrt x }}$, hence $y'' = \displaystyle{3 \over {2\sqrt 4 }} = \displaystyle{3 \over 4}$; and

   $\displaystyle{{{dD} \over {dt}}} = \displaystyle{{x\displaystyle{{dx} \over {dt}} + y{{dy} \over {dt}}} \over {\sqrt {{x^2} + {y^2}} }} = {{4(3) + 2\left( \displaystyle{{3 \over 4}} \right)} \over {\sqrt {20} }} = {{18} \over {2\sqrt 5 }}$

   The distance is increasing at a rate of $\displaystyle{{{18} \over {2\sqrt 5 }}}$ cm/s.

6. A plane flying horizontally at an altitude of $1$ mi and a speed of $500$ mi/h passes directly over a radar station. Find the rate at which the distance from the plane to the station is increasing when the plane is $2$ mi away from the station.

   Mistake

   Here $y$ and $x$ change with respect to time and the differentiation is incorrect; also, by putting the rate of $x$ in the diagram the substitution is incorrect.

   Solution

   We want $\displaystyle{\frac{dy}{dt}}$ when $y = 2$ mi.

   

   Figure 10. Correct solution to “Learning from Mistakes” Question 3(a).

   From the figure, $y^2 = x^2 + 1$. Differentiating yields

   $\displaystyle{2y \frac{dy}{dt} = 2x\frac{dx}{dt}}$

   and solving gives us

   $\displaystyle{\frac{dy}{dt} = \left(\frac{x}{y}\right)\left(\frac{dx}{dt}\right)}.$

   When $y = 2$ we have that $x = \sqrt{3}$ and $\displaystyle{\frac{dx}{dt}} = 500$~mi/h, then

   $\displaystyle{\frac{dy}{dt} = \frac{\sqrt{3}}{2}(500) = 250\sqrt{3}}.$

   The distance is increasing at a rate of $250\sqrt{3}$ mi/h.

Unit 5

1. Sketch the graph of the function $f(x) = (x - 1)^{3/2}$.

   Mistake

   The mistake is in ignoring the domain of the function, and the $x$ and $y$ intercepts.

   Solution

   1. The domain is the interval $[1,\infty)$
   2. No $y$-intercept (why?), and $f(1) = 0$, hence $(1,0)$ is the $x$-intercept.
   3. The function cannot have symmetries (why?)
   4. No asymptotes (why?)
   5. $f'(x) = (3/2)(x - 1)^{1/2}$ the critical number is $x = 1$ because $f'(1) = 0$. Since $f'(x) \gt 0$ for all $x \ge 1$, the function is increasing on $(0,\infty)$. Hence no local extreme values.
   6. $f''(x) = 3/4(x - 1)^{-1/2}$ and $f''(x) \gt 0$ for all $x \gt 1$, the function is concave up on its domain.

   

   Figure 11. Correct solution to “Learning from Mistakes” Question 1.

2. Find the local extreme points of the function $g(x)= x^6 + 6x^4$.

   Mistake

   The Second derivative test is inconclusive in this case because $g''(0) = 0$, hence we need to use the intervals of increase and decrease of the function.

   Solution

   It is true that the only critical number is $x = 0$ because $g'(x)= 6x^5 + 24x^3 = 6x^3(x^2 + 4)$ and $g(0) = 0$ and $x^2 + 4 \gt 0$ for all $x$.

   But we have that $g'(x) \lt 0$ for $x \lt 0$ and $g'(x) \gt 0$ for $x \gt 0$, hence the function has a local minimum at $x = 0$.

3. Find the extreme values of the function $h(x) = x^3 - 6x$ on the interval $[0,2]$.

   Mistake

   The value $-\sqrt{2}$ which is not in the interval $[0,2]$.

   Solution

   Since $h'(x) = 3x^2 -6$ it is true that $x = \sqrt{2}$ and $x = -\sqrt{2}$ are the critical numbers, but only $\sqrt{2}$ is in the interval $[0,2]$.

   Thus $h(\sqrt{2}) = (\sqrt{2})^3 - 6\sqrt{2} \approx -5.656$.

   The values at the endpoints are $h(0) = 0$ and $h(2) = -4$.

   By the closed interval method the absolute minimum value is $(\sqrt{2})^3 - 6\sqrt{2} \approx -5.656$ at $x = \sqrt{2}$ and the absolute maximum value is 0 at $x = 0$.

4. Find a number greater or equal to 2 such that the sum of the number and its reciprocal is as small as possible.

   Mistake

   The answer has to be a number greater or equal to 2.

   Solution

   Let $x$ be such a number. Hence we want to minimize the function

   $f(x) = x + \displaystyle{\frac{1}{x}}$ with $x$ in the interval $[2,\infty)$.

   Since $f'(x) = 1 -\displaystyle{\frac{1}{x^2}} = 0$ if $x = 1$ or $x = -1$

   and both are less than 2 the number we are looking for is not a critical number.

   Since $f'(x) \gt 0$ for all $x \geq 2$ the function is increasing on $[2,\infty)$, hence the minimum is at $x = 2$, and this is the answer.

Unit 6

1. Integrate $\displaystyle{\int \tan^2(3x)\sec^2(3x)\,dx}$.

   Mistake

   The derivative of $f$ is $f'(x) = 3\sec^2(3x)$.

   Solution

   $f(x) = \tan(3x)$, $r = 2$ and $f'(x) = 3\sec^2(3x),$

   then

   $\displaystyle{\frac{1}{3} \int 3\tan^2(3x)\sec^2(3x)\,dx = \frac{\tan^3(3x)}{9}} + C.$

2. Integrate $\displaystyle{\int_1^5 x^3\sqrt{x^2 + 1}\;dx}$.

   Mistake

   The limits of integration have to change according to the function $u$.

   Solution

   Let $u = x^2 + 1$, $du = 2u\,dx$, $x^2 = u - 1$. If $x = 1$, $u = 2$ and if $x = 5$, $u = 26$, then

   \begin{align*} \frac{1}{2}\int_2^{26} (u - 1)u^{1/2}\,du & = \frac{1}{2} \int_2^{26} u^{3/2} - u^{1/2}\,du \\ & = \frac{u^{5/2}}{5} - \frac{u^{3/2}}{3}\Bigg|_2^{26} \\ & = \frac{(26)^{5/2}}{5} - \frac{(26)^{3/2}}{3} - \left(\frac{2^{5/2}}{5} - \frac{2^{3/2}}{3}\right) \\ & = \sqrt{8}\left(\frac{73\sqrt{13^3} - 1}{15}\right) \end{align*}

3. Integrate $\displaystyle{\int_0^1 (x^2 - \sqrt{x})^2\;dx}$.

   Mistake

   The evaluation of the limits of integration is incorrect.

   Solution

   \begin{align*} \int_0^1 (x^2 - \sqrt{x})^2\;dx & = \int_0^1 x^4 - 2x^{5/2} + x \,dx \\ & = \frac{x^5}{5} - \frac{4x^{7/2}}{7} + \frac{x^2}{2} \Bigg|_0^1 \\ & = \left(\frac{1}{5} - \frac{4}{7} + \frac{1}{2}\right) \\ & = \frac{9}{70} \end{align*}

4. Find a single function $f(x)$ that satisfies the following two conditions:

   1. $f'(x) = \cos x + \sqrt{3x}$, and
   2. $f(1) = 1$.

   Mistake

   The constant of integration is missing.

   Solution

   To find $f$ we integrate its derivative

   $\displaystyle{\int \cos x + \sqrt{3}\sqrt{x}\,dx = \sin x + \frac{2\sqrt{3}x^{3/2}}{3} + C}$

   $\displaystyle{f(x) = \sin x + \frac{2\sqrt{3}x^{3/2}}{3} + C}$

   $\displaystyle{f(1) = \sin(1) + \frac{2\sqrt{3}}{3} + C = 1}$

   solving for $C$, the answer is

   $\displaystyle{f(x) = \sin x + \frac{2\sqrt{3}x^{3/2}}{3} + \frac{3 - 2\sqrt{3}}{3} - \sin(1)}$.

5. Let $f(x) = 4x^3 - 6x^2 + 3$ be a continuous function. Find the value $c$ in the interval $[-1,0]$ which satisfies the Mean Value Theorem.

   Mistake

   Only one of the values found is in interval $[-1,0]$.

   Solution

   $f'(x) = 12x^2 - 12x$ and $\displaystyle{\frac{f(0) - f(-1)}{0 - (-1)} = 10}$; hence, $12x^2 - 12x = 10$ and solving for $x$ (using the quadratic formula) $x = \displaystyle{\frac{3 \pm \sqrt{39}}{6}}$. The value $x = \displaystyle{\frac{3 - \sqrt{39}}{6}}$ in the interval $[-1,0]$ satisfies the Mean Value Theorem.

6. Find the area below the curve of the function $f(x) = x^3 + 4x$ on the interval $[-1,3]$.

   Mistake

   The area under the curve is given by two integrals, one for the interval where the function is negative and another where the function is positive.

   Solution

   The function $f(x) = x(x^2 + 4)$ is negative for $x \lt 0$ and positive for $x \gt 0$. Hence the area under this curve in the interval $[-1,3]$ is given by the integrals

   \begin{align*} -\int_{-1}^0 x^3 + 4x\,dx + \int_0^3 x^3 + 4x\,dx & = -\left(\frac{x^4}{4} + 2x^2\right)\Bigg|_{-1}^0 + \left(\frac{x^4}{4} + 2x^2 \right)\Bigg|_0^3 \\ & = \left(\frac{1}{4} - 2\right) + \left(\frac{3^4}{4} -2(3)\right) \\ & = 40.5 \end{align*}

   The area is $40.5$.

7. Find the derivative of the function $g(x) = \displaystyle{\int_{3x}^4 t\tan t\,dt}$.

   Mistake

   Part 1 of the Fundamental Theorem of Calculus is applied incorrectly, and the derivative of the lower limit of integration is missing.

   Solution

   $g'(x) = -\displaystyle{\frac{d}{dx} \int_4^{3x} t\tan t\,dt = -(9x)\tan(3x)}$.

Unit 7

1. A spacecraft uses a sail and the “solar wind” to produce a constant acceleration of 0.032 m/s$^2$. Assuming that the spacecraft has a velocity of 600 km/h when the sail is first raised, how far will the spacecraft travel in 1 hour, and what will its velocity be at the end of this hour?

   Mistake

   Units are not properly used.

   Solution

   We define $t_0 = 0$ to be the time the sail is raised, $t_1 = 1$ one our later, the acceleration $a = 0.032$, and at time $t$ the velocity is $v(t)$ and displacement is $s(t)$. We then have $s(0) = 0$ and $v(0) = 600$ km/h. We choose metres and seconds, hence $v(0) = 166.66$ m/s and $t_1 = 3600$.

   Hence $v(t) = 166.66 +.032t$, and $v(3600) = 166.66 + .032(3600) = 281.86$.

   \begin{align*} s(3600) - s(0) = s(3600) & = \int_0^{3600}166.66 + .032t\,dt\\ & = 166.66t + .016t^2\Big|_0^{3600} \\ & = 166.66(3600) + .016(3600)^2\\ & = 807336. \end{align*}

   Answer: Velocity is $281.86$ m/s or $807 336$ km/h and the distance is $807 336$ m or $807.336$ km.

2. Find the area under the curve $y = x^2 + x - 2$ on the interval $[0,3]$.

   Mistake

   The function given is negative on the interval $[0,1]$ and positive on $[1,3]$. Hence the area under the curve is given by two integrals.

   Solution

   $\displaystyle{-\int_0^1 x^2 + x - 2\,dx = -\frac{x^3}{3} - \frac{x^2}{2} + 2x\bigg|_0^1 = \frac{7}{6}}$.

   $\displaystyle{\int_1^3 x^2 + x -2\,dx = \frac{x^3}{3} +\frac{x^2}{2} - 2x\bigg|_1^3 = \frac{26}{3}}$.

   The area is $\displaystyle{\frac{7}{6}} + \displaystyle{\frac{26}{3}} = \displaystyle{\frac{59}{6}}$.

3. Find the area between the curves $y = \displaystyle{\frac{1}{x^2}}$, $y = x$ and $y = \displaystyle{\frac{x}{8}}$.

   Mistake

   The area is given by two integrals and in each one of them we must take the difference between the function that is above minus the curve that it is below.

   Solution

   Point of intersection of $y = \displaystyle{\frac{1}{x^2}}$ and $y = x$ is the solution of $x = \displaystyle{\frac{1}{x^2}}$; that is, $x = 1$. Hence, $(1,1)$. Point of intersection of $y = \displaystyle{\frac{1}{x^2}}$ and $y = \displaystyle{\frac{x}{8}}$ is the solution of $(x^2)\displaystyle{\frac{x}{8}} = 1$ that is $x = 2$ and $(2,1/4)$.

   On the interval $[0,1]$ the line $y = x$ is above the curve $y = \displaystyle{\frac{x}{8}}$; hence, the area is

   $\displaystyle{\int_0^1 x - \frac{x}{8} = \frac{7}{8}\int_0^1 x\,dx = \left(\frac{7}{8}\right)\frac{x}{2}\Bigg|_0^1 = \frac{7}{16}}$.

   On the interval $[1,2]$ the curve $y=\displaystyle{\frac{1}{x^2}}$ is above the line $y = \displaystyle{\frac{x}{8}}$, hence the area is

   $\displaystyle{\int_1^2 \frac{1}{x^2} - \frac{x}{8} = - \frac{1}{x} - \frac{x^2}{16}\Bigg|_1^2 = \frac{5}{16}}$.

   The answer is $\displaystyle{\frac{7}{16}} + \displaystyle{\frac{5}{16}} = \displaystyle{\frac{12}{16}} = \displaystyle{\frac{3}{4}}$.

4. A spring exerts a force of 100 N when it is stretched 0.2 m beyond its natural length. How much work is required to stretch the spring 0.8 m beyond its natural length?

   Mistake

   The spring constant has to be found using Hooke’s Law before finding work. Also the spring is stretched from 0 to 0.8 m.

   Solution

   The force is $F = kx$ by Hooke’s Law. Hence $100 = k(.2)$ and we have that the spring constant is $k = 500$ N/m.

   $W = \displaystyle{\int_0^{.8} 500x\,dx = 250x^2\Big|_0^{.8} = 250(.64) = 160}$.

   The answer is 160 J.