Mathematics 265 Introduction to Calculus I
Solutions to Sample Midterm Exam
Sample Midterm Examination 2
Time: 3 hours
Passing grade: 55%
Total points: 64
Solutions and Marking Scheme
These are our solutions. Your solutions may be different but equally correct. If you have any doubts, consult your tutor. Full credit is given if
- the question is answered: you find what we are asking for, you describe what we are asking for, and you gave what we are asking for.
- the answer is correct.
- you explain and/or justify each of your steps.
- (4 points)
Determine which of the following equations are well defined functions with an independent variable . Explain.
Solution
If we solve for , we get . (1 pt)
Hence, this is an algebraic function and is well defined for any , therefore for every there is one and only one value of and the function is well defined. (1 pt)
it is not, (1 pt)
because and satisfy the equation. (1 pt)
- (4 points)
- Consider a cone whose height is double the size of its radius.
- Express the volume of the cone as a function of radius .
- Find the domain of the function in a.
- Use the function in a. to compute the volume of the cone for .
Hint: The volume of a cone is .
Solution
Since , (1 pt)
we have . (1 pt)
Since is the radius, the domain is . (1 pt)
. (1 pt)
- (4 points)
- The population of a city in the year is . Write a sentence (in layman’s terms) that explains the meaning of the expressions
- .
Solution
this is the average on the interval , (1 pt)
hence from the years 2 to 15, on average the population is increasing at a rate of 1,431 people per year. (1 pt)
is an instant rate of change. (1 pt)
Hence, in the 10th year, the population is increasing at a rate of 14,000 people per year. (1 pt)
- (6 points)
Indicate the transformations in the order they are applied to the basic graph of in the interval in order to obtain the graph of the function . Apply the transformations to sketch the graph of , no credit will be given if other method is used.
Solution
Shift to the right by 2 units gives . (1 pt)
Reflection with respect to the -axis gives . (1 pt)
Vertical stretch by 3 units gives . (1 pt)
The graph is
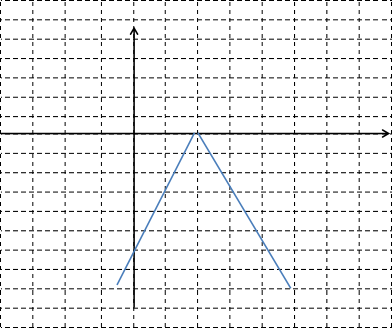 (3 pts)
(3 pts)- (10 points)
- Interpret in terms of the graph of the function the conditions listed below. Sketch the graph of a single function which satisfies all of the conditions listed below.
lim x → − 1 f ( x ) = 2 lim x → 1 f ( x ) = ∞ - the function is continuous but not differentiable at
x = 0
Solution
lim x → ∞ f ( x ) = 3 y = 3 f ( 0 ) = 0 ( 0 , 0 ) lim x → − 1 f ( x ) = 2 − 1 2 lim x → 1 f ( x ) = ∞ 1 the function is continuous but not differentiable at
x = 0 ( 0 , 0 )
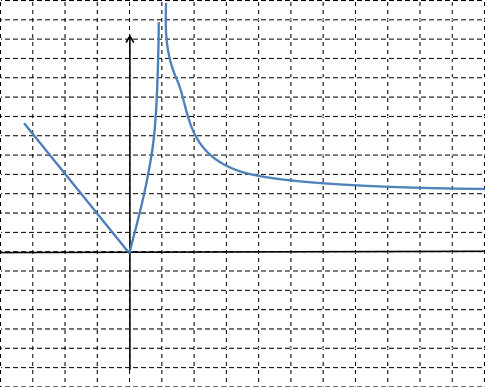 (3 pts)
(3 pts) - (10 points)
Find the vertical and horizontal asymptotes of the function
f ( x ) = x 2 − 3 x − 4 x 2 − 1 6 . Solution
Vertical Asymptotes.
x 2 − 1 6 = ( x − 4 ) ( x + 4 ) x = 4 , x = − 4 x 2 − 3 x − 4 x 2 − 1 6 = ( x + 1 ) ( x − 4 ) ( x + 4 ) ( x − 4 ) = x + 1 x + 4 lim x → − 4 + ( x 2 − 3 x − 4 ) 2 x 2 − 16 = lim x → − 4 + x + 1 x + 4 = − ∞ because
lim x → − 4 x + 1 = − 3 < 0 x + 4 > 0 x → − 4 + lim x → − 4 + x + 4 = 0 The only vertical asymptote is
x = − 4 Horizontal Asymptotes.
lim x → ∞ ( x 2 − 3 x − 4 ) 2 x 2 − 16 = 1 lim x → − ∞ ( x 2 − 3 x − 4 ) 2 x 2 − 16 = 1 because the degrees of the numerator an denominator are equal. (1 pt)
So
y = 1
- (24 points)
Evaluate each of the limits given below. If a limit does not exist, explain why.
Note: No credit will be given for unjustified answers.
lim x → 1 x 2 − 1 x 3 − 1 lim x → 0 x 2 1 − cos ( 2 x ) lim x → 0 6 x − 9 x 3 − 1 2 x + 3 lim x → ∞ 5 − 2 x 3 x 2 + 2 lim x → − π / 3 tan ( 2 x ) 3 x + π lim x → 2 cos ( π x ) ( x − 2 ) 2
Solution
x 2 − 1 x 3 − 1 = ( x − 1 ) ( x + 1 ) ( x − 1 ) ( x 2 + x + 1 ) = x + 1 x 2 + x + 1 lim x → 1 x 2 − 1 x 3 − 1 = lim x → 1 x + 1 x 2 + x + 1 = 2 3 We use the identity
1 − cos 2 a = sin 2 a x 2 1 − cos ( 2 x ) = x 2 1 − cos ( 2 x ) ( 1 + cos ( 2 x ) 1 + cos ( 2 x ) ) x 2 1 − cos ( 2 x ) = x 2 ( 1 + cos ( 2 x ) ) 1 − cos 2 ( 2 x ) x 2 1 − cos ( 2 x ) = x 2 ( 1 + cos ( 2 x ) ) sin 2 ( 2 x ) x 2 1 − cos ( 2 x ) = ( x sin ( 2 x ) ) 2 ( 1 + cos ( 2 x ) ) By the law of limits and trigonometric limit
lim x → 0 x sin ( 2 x ) = 1 2 lim x → 0 x 2 1 − cos ( 2 x ) = lim x → 0 ( x sin ( 2 x ) ) 2 ( 1 + cos ( 2 x ) ) = 2 4 = 1 2 The function
6 x − 9 x 3 − 1 2 x + 3 0 Hence,
lim x → 0 6 x − 9 x 3 − 1 2 x + 3 = − 9 3 = − 3 The function
5 − 2 x 3 x 2 + 2 lim x → ∞ 5 − 2 x 3 x 2 + 2 = lim x → ∞ − 2 x 3 x 2 = lim x → ∞ − 2 x = − ∞ The function is not continuous at
− π / 3 tan ( − 2 π 3 ) = − 3 < 0 lim x → − π / 3 − 1 3 x + π = − ∞ lim x → − π / 3 + 1 3 x + π = ∞ because
3 x + π < 0 x → − π / 3 − 3 x + π > 0 x → − π / 3 + Hence
lim x → − π / 3 − tan ( 2 x ) 3 x + π = ∞ lim x → − π / 3 + tan ( 2 x ) 3 x + π = − ∞ so the limit does not exist. (2 pts)
The function is not continuous at 2.
lim x → 2 1 ( x − 2 ) 2 = ∞ because
( x − 2 ) 2 > 0 x ≠ 2 lim x → 2 ( x − 2 ) 2 = 0 Since
lim x → 2 cos ( π x ) = cos ( 2 π ) = 1 > 0 we conclude that
lim x → 2 cos ( π x ) ( x − 2 ) 2 = ∞
- (6 points)
Use linearization to estimate the value of
sin ( 62 ° ) Solution
We set
f ( x ) = sin x a = 60 ° = π 3 Δ x = 2 ° = π 90 f ( a + Δ x ) ≈ f ′ ( a ) Δ x + f ( a ) = cos ( π 3 ) ( π 90 ) + sin ( π 3 ) We have
sin ( 62 ° ) ≈ π 180 + 3 2 - (16 points)
Find each of the derivatives listed below. Show your work.
Note: You may not need to simplify your answer.
d 2 d x 2 cot ( 2 x ) d d x sec ( x 2 − 3 x ) d d x x 2 − cos ( 3 x ) x sin ( 2 x ) d d x f ( x ) g ( x ) | x = 1 f ( 1 ) = 3 g ( 1 ) = 6 f ′ ( x ) = x g ′ ( x ) = 3 sin ( π x / 3 )
Solution
d d x cot ( 2 x ) = − 2 csc 2 ( 2 x ) d 2 d x 2 cot ( 2 x ) = d d x − 2 csc 2 ( 2 x ) d 2 d x 2 cot ( 2 x ) = − 2 ( − 2 csc ( 2 x ) cot ( 2 x ) csc ( 2 x ) ( 2 ) ) d 2 d x 2 cot ( 2 x ) = 8 csc 2 ( 2 x ) cot ( 2 x ) d d x sec ( x 2 − 3 x ) = sec ( x 2 − 3 x ) tan ( x 2 − 3 x ) ( 2 x − 3 ) f ( x ) = x 2 − cos ( 3 x ) g ( x ) = x sin ( 2 x ) Thus,
f ′ ( x ) = 2 x + 3 sin ( 3 x ) g ′ ( x ) = sin ( 2 x ) + 2 x cos ( 2 x ) d d x x 2 − cos ( 3 x ) x sin ( 2 x ) = x sin ( 2 x ) [ 2 x + 3 sin ( 3 x ) ] − ( x 2 − cos ( 3 x ) ) [ sin ( 2 x ) + 2 x cos ( 2 x ) ] x 2 sin 2 ( 2 x ) By the quotient rule
d d x f ( x ) g ( x ) | x = 1 = f ′ ( x ) g ( x ) − f ( x ) g ′ ( x ) g ( x ) 2 | x = 1 d d x f ( x ) g ( x ) | x = 1 = f ′ ( 1 ) g ( 1 ) − f ( 1 ) g ′ ( 1 ) g ( 1 ) 2 | x = 1 f ′ ( 1 ) = 1 = 1 g ′ ( 1 ) = 3 sin ( π / 3 ) = 3 3 2 Thus,
d d x f ( x ) g ( x ) | x = 1 = 6 − 9 3 2 36 = 2 − 3 3 12
- (4 points)
Find the equation of the tangent line to the curve
y 3 + y x 2 + x 2 = 3 y 2 ( 1 , 1 ) Solution
By implicit differentiation
3 y 2 y ′ + x 2 y ′ + 2 x y + 2 x = 6 y y ′ x = 1 y = 1 4 y ′ + 4 = 6 y ′ Solving for
y ′ = 2 y − 1 = 2 ( x − 1 ) y = 2 x − 1 - (6 points)
A rocket, rising vertically, is tracked by a radar station that is on the ground 5 mi from the launch pad. How fast is the rocket rising when it is 4 mi high and its distance from the radar station is increasing at a rate of 2000 mi/h?
Solution
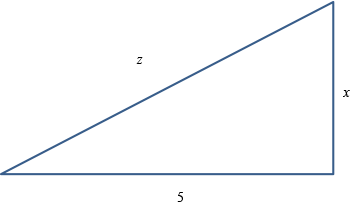 (2 pts)
(2 pts)According to the diagram, we want to know
d x d t x = 4 d z d t = 2 0 0 0 By Pythagoras theorem,
z 2 = 25 + x 2 2 z d z d t = 2 x d x d t x = 4 z = 41 2 41 ( 2000 ) = 2 ( 4 ) d x d t d x d t = 500 41 mi/hr
